



STAND JUSSIEU
Manipulations
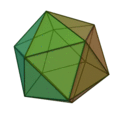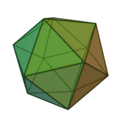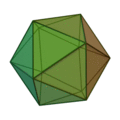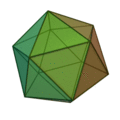
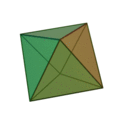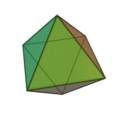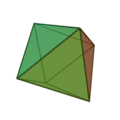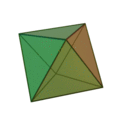
On ne peut construire que 9 solides réguliers.









La démonstration du fait qu'il n'en existe que 9 est très compliquée. Pour les polyèdres convexes (i.e pour lesquels toutes ses diagonales sont contenues à l'intérieur du polyèdre) il existe une démonstration qui repose sur la caractéristique d'Euler des polyèdres, vous pouvez la trouver à l'adresse suivante:
http://www.eleves.ens.fr/home/pilaud/enseignement/agreg/polyedres/polyedres.pdf .
Questions
Avant toute chose il convient de rappeler les définitions.
Soient n points quelconques du plan M1, ..., Mn, tous distincts. On appelle polygone à n côtés la figure formée par les n segments (appelés côtés) : MiMi+1, pour i allant de 1 à n-1, et MnM1.
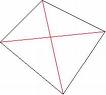
Pour un quadrilatère on a n=4, donc 4(4-3)/2=2 diagonales.
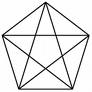
Pour un pentagone on a n=5, donc 5(5-3)/2=5 diagonales.
Pour un octogone on a n=8, donc 8(8-3)/2=20 diagonales.
Pour un décagone on a n=10, donc 10(10-3)/2=35 diagonales.